Basic algebra
0.1. - BASIC LOGIC
Is any statement of which is true if it is true or false, but not both at once. If a statement is true is assigned the letter V (or value 1) and if false, the letter F (or 0).
Tautology is a proposition that is always true.
Absurd a proposition that is always false.
Is any statement of which is true if it is true or
false, but not both at once. If a statement is true is assigned the letter V (or value 1) and if false, the letter F (or 0).
T
• Disjunction: p or q (p ∨ q).
• Conjunction: p and q (p ∧ q).
• Implication: p ⇒ q (p → q). It reads: If p then q.
• Double implication: p ⇔ q (p ↔ q). It reads: p iff q.Los operating results propositions are logically
determined by the truth values assigned to them, which depend on having the starting propositions. These are usually represented in so-called "truth tables". Truth tables defined above propositions are:
outlook
Propositional function:
If p (x) is an expression that becomes proposition by substituting x by a mathematical object, then we say that p is a propositional function. There is also propositional functions over a mathematical object (p (x, y) p(x, y, z), ...).
QUANTIFIERS
• Universal: If p (x) is a proposition that is true for any x, then write ∀ x, p (x), which is read "for all x is verified p"
• Existential:
a) If p (x) is a true proposition ever for at least some x, then write x, p (x), which is read "there exists at least one x for which verifies p"
b)If p (x) is a true proposition for a single x, then write ∃ x, p (x), which reads "there is only one x for which it verifies p"
THEOREMS
In a mathematical theory, called theorems true propositions concerning mathematical objects of the same. Theorems are often enunciate as implications, and the implications that being true propositions are theorems. Generally, the terms theorem and involvement are considered equivalent.
o DEMONSTRATION: The logical process, from a proven proposition p, leads to the truth of another proposition q, is the proof of the theorem p ⇒ q. The proof of a theorem can be done in several ways:
• Direct: If certain py and p ⇒ q, then so is q.
• contrapositive: involves in proving that (not q) ⇒ (not p), rather than to prove p ⇒ q.
• Reduction to the absurd: is to assume that q is false, so the hypothesis becomes p (not q) and prove that it follows a contradiction. '
„
„„o Refutation Disproving theorem alleging p ⇒ q ,is proven to be false, what is indicated by putting p ⇒ Not q. To do this, we may assume that p and q are true and find from this a contradiction, or finding a counterexample, ie given a particular case in which p is true and q is false.
2 Set Theory
TEORÍA DE CONJUNTOS
Set
It defines a set as a collection or gathering of well-defined and distinct elements. Usually capital letters are used to designate a set. Can be expressed in two ways:
• By extension: Indicating each and every one of its elements. Usually write the elements of the set in braces ({...}).
• By realization: Giving a property that met all the elements of the set and only them. To indicate that an item "belongs" to a set using the symbol of belonging, ∈.
• By realization: Giving a property that met all the elements of the set and only them. To indicate that an item "belongs" to a set using the symbol of belonging, ∈.
SUBSET
A set S is a subset of another set C if all elements of S are elements of C. In this case the set S is also called "part" of C. To indicate this we use the symbol of inclusion, ⊂ ⊃; (S ⊂C , C ⊃ S). The inclusion of sets may be understood in two ways:
• Broadly: C ⊆ S.
• Strictly: C ⊂ S.
Empty set: The set that has no elements. It is denoted by ∅
UNIVERSAL JOINT OR FOR REFERENCE
It is the Set to which contains"all" item, which all sets are subsets. It is denoted by I (belong to U).
Note: This is a reference that owns all the elements of the sets emerged in a situation or problem. If a universal joint is regarded also what are all sets that contain it.
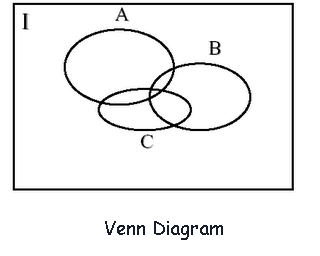
VENN DIAGRAMS:
They are represented in the level of the joint.
Set Operations:
• UNION A∪B = { x / x ∈A o x ∈ B }
• INTERSECTION A ∩ B = {x / x ∈ A and x ∈ B }
• DIFFERENCE A−B = {x / x ∈ A And ∉ B }
• SYMMETRIC DIFFERENCE A ∆ B= ( A − B) ∪( B − A)
Properties of the union and intersection:
A∪ ( B∪ C ) = (A ∪ B) ∪ C
A ∩ ( B ∩ C ) = (A ∩ B) ∩ C
• Commutative
A ∪ B = B ∪ A
A ∩ B = B ∩ A
• Idempotent

A ∪ A = A
A ∩ A = A
• Absolution

A ∪ I = I
A ∩ ∅ = ∅
• Simplification:

A ∪ ( A ∩ B) = A
A ∩ ( A ∪ B) = A
• Distributive:

A ∪( B ∩ C) = (A ∪ B) ∩ (A ∪ B)
A ∩ (B ∪ C ) = (A ∩ B) ∪ (A ∩ C)
Disjoint and Complementary Sets
Disjoint sets: Two or more sets are called disjoint sets if their intersection is Empty set
( A ∩ B ∩ ......) = ∅
Complementary Set Two or more sets are called complementary when their union equal the universal Set
(A∪B ∪ .....= I) . The complement Set A is denoted by Ac
Properties
•Complementarities:

A ∪ Ac = I
A ∩ Ac =∅
•
Package of parts of a Set Given a set A, is called set of parts of A and is denoted by P(A) to another set whose elements are all possible subsets or portions of A
P( A ) = {B / B ⊆ A}
Covering set Given a set and a family of subsets A1,A2 ,.......,An (finite or not) .It is said this family is covering set if A1∪ A2 ∪ .....∪ An = A
Partition of a set A partition of a set A is also a covering verifying that
Ai ∩ Aj = ∅ ∀ i ≠ j .
i
Disjoint sets and complementary
Cardinal of a finite set: It is the number of elements have the assembly .It is generally represented
N(X) or cardX
The most common formulas, not the only, that relate the cardinal and operations between sets are
N (A ∪ B) =N( A) + N( B) − N(A ∩ B)
N(Ac ) = N(I) - N(A)
N( A − B )=N(A)- N(A∩ B)
Being N(I) the total number of elements of of reference and taking note that N (∅) = 0.
0.3. - APPLICATIONS
Cartesian product:
Set is defined in Cartesian product by two sets A and B and is denoted by A*B set of ordered pairs(a,b) where a ∈ A and b ∈ B that is to say:
A× B ={(a,b), ∀a ∈A and ∀b ∈B}
The elements of the first set "source" correspond to elements of the second set "image":
Is any subset of the Cartesian product:
A× B ⊇ G = {(a, / b) a ∈ A, b ∈B}
The elements of the first set "source" correspond to elements of the second set "image":
APPLICATION:
It is a correspondence that verifies:
x ∈ A ∃ | y ∈B /(x, y) ∈ G
Applications, also called "tasks" are usually represent by the letters f, g,, h, ...,,, F,G,H, ..., and are represented by:
f
f A: → B Or A → B
so we can express the application definition:
x ∈A ∃ | y ∈ B y = f ( x)
Application domain: It is the subset of source array elements for which there is an image:
Domf =x ∈ {A / y, ∃∈B, y = f(x)}
Application Image :Is the subset of the set of image elements which have their origin
Im f = {y ∈ B /∃ x ∈ A , y = f (x) } = f(x)
TYPES OF APPLICATIONS:
surjective: Every element of the whole image has "at least" one source:
∀y ∈ B , ∃x ∈ A / y = f (x)
injective: Different elements in the original group have distinct images in the image set:
∀x, z, ∈ A / x ≠ z ⇒ f (x) ≠ f (z)
bijective: When it is surjective and injective at once:
∀y ∈ B , ∃ | x ∈ A / y = f (x)
COMPOSITION OF APPLICATIONS:
Given the applications, f: A → B And g:B → C,verifying that Im f⊂ D ⊂ omg ,You can define the Application Composition h= g D f in the form
h: A →C/∀ x ∈ A , h(x) = (g D f )(x) = g[ f (x)]
Properties
• No type is empty, with a ∈ cl ()
• Items belonging to the same class are interrelated.
• Classes are disjoint, since if two classes have a common element is that they are the same class. Therefore, an equivalence class is defined by "any" of its elements.
Conclusion: When defining an equivalence relation on a set, every element of the set is in a class and only one.
Order relationships
They can be of two types
BROAD: If you meet the properties reflexive, antisymmetric and transitive.
STRICT: If you meet antisymmetric and transitive properties.
• UNION A∪B = { x / x ∈A o x ∈ B }
• INTERSECTION A ∩ B = {x / x ∈ A and x ∈ B }
• DIFFERENCE A−B = {x / x ∈ A And ∉ B }
• SYMMETRIC DIFFERENCE A ∆ B= ( A − B) ∪( B − A)
Properties of the union and intersection:
∎ Associative A ∪ B = {x / x ∈ A OR x ∈B }
∎ INTERSECTION A ∩ B = {x / x ∈ A AND x ∈B}
∎ DIFFERENCE : A − B = {x /x ∈ A AND x ∉B }
∎ SYMMETRIC DIFFERENCE A ∆ B= ( A − B) ∪( B − A)
A ∩ ( B ∩ C ) = (A ∩ B) ∩ C
• Commutative
A ∪ B = B ∪ A
A ∩ B = B ∩ A
• Idempotent
A ∪ A = A
A ∩ A = A
• Absolution
A ∪ I = I
A ∩ ∅ = ∅
• Simplification:
A ∪ ( A ∩ B) = A
A ∩ ( A ∪ B) = A
• Distributive:
A ∪( B ∩ C) = (A ∪ B) ∩ (A ∪ B)
A ∩ (B ∪ C ) = (A ∩ B) ∪ (A ∩ C)
Disjoint and Complementary Sets
Disjoint sets: Two or more sets are called disjoint sets if their intersection is Empty set
( A ∩ B ∩ ......) = ∅
Complementary Set Two or more sets are called complementary when their union equal the universal Set
(A∪B ∪ .....= I) . The complement Set A is denoted by Ac
Properties
•Complementarities:
A ∪ Ac = I
A ∩ Ac =∅
•
Package of parts of a Set Given a set A, is called set of parts of A and is denoted by P(A) to another set whose elements are all possible subsets or portions of A
P( A ) = {B / B ⊆ A}
Covering set Given a set and a family of subsets A1,A2 ,.......,An (finite or not) .It is said this family is covering set if A1∪ A2 ∪ .....∪ An = A
Partition of a set A partition of a set A is also a covering verifying that
Ai ∩ Aj = ∅ ∀ i ≠ j .
i
Disjoint sets and complementary
Cardinal of a finite set: It is the number of elements have the assembly .It is generally represented
N(X) or cardX
The most common formulas, not the only, that relate the cardinal and operations between sets are
N (A ∪ B) =N( A) + N( B) − N(A ∩ B)
N(Ac ) = N(I) - N(A)
N( A − B )=N(A)- N(A∩ B)
Being N(I) the total number of elements of of reference and taking note that N (∅) = 0.
0.3. - APPLICATIONS
Cartesian product:
Set is defined in Cartesian product by two sets A and B and is denoted by A*B set of ordered pairs(a,b) where a ∈ A and b ∈ B that is to say:
A× B ={(a,b), ∀a ∈A and ∀b ∈B}
The elements of the first set "source" correspond to elements of the second set "image":
Is any subset of the Cartesian product:
A× B ⊇ G = {(a, / b) a ∈ A, b ∈B}
The elements of the first set "source" correspond to elements of the second set "image":
APPLICATION:
It is a correspondence that verifies:
x ∈ A ∃ | y ∈B /(x, y) ∈ G
Applications, also called "tasks" are usually represent by the letters f, g,, h, ...,,, F,G,H, ..., and are represented by:
f
f A: → B Or A → B
so we can express the application definition:
x ∈A ∃ | y ∈ B y = f ( x)
Application domain: It is the subset of source array elements for which there is an image:
Application Image :Is the subset of the set of image elements which have their origin
Im f = {y ∈ B /∃ x ∈ A , y = f (x) } = f(x)
TYPES OF APPLICATIONS:
surjective: Every element of the whole image has "at least" one source:
∀y ∈ B , ∃x ∈ A / y = f (x)
injective: Different elements in the original group have distinct images in the image set:
∀x, z, ∈ A / x ≠ z ⇒ f (x) ≠ f (z)
bijective: When it is surjective and injective at once:
∀y ∈ B , ∃ | x ∈ A / y = f (x)
COMPOSITION OF APPLICATIONS:
Given the applications, f: A → B And g:B → C,verifying that Im f⊂ D ⊂ omg ,You can define the Application Composition h= g D f in the form
h: A →C/∀ x ∈ A , h(x) = (g D f )(x) = g[ f (x)]
Applications, also called "functions" are usually represented by the letters letters, and are represented by:
Domain of the application: Is the subset of the set of elements for which there is home image
The application image: Is the subset of the set of image elements which have their origin
Types of Applications
surjective Every element of the whole picture has "at least" one source:
Structure of applications
Inverse mapping: Given an application, f A: → B, if you can define another application ƒ−1: B → A such that if y f(x) ⇔ x = ƒ−1 (y) . The ƒ−1 application is called inverse or reciprocal f is verified:
0.4 Binary relations
Binary relation defined on a set to any subset of the Cartesian product AxA and
R⊂ AxA
Properties
The binary relations can have the following propertiesif
•Reflexive:: a Ra , ∀a ∈ A
•Symmetric: if a Rb ⇔ bRa
•Antisymmetric: if a Rb and bRa ⇒ a = b
•Transitive :if a Rb and bRc ⇒ aR
c•Associated : if a Rb ó bRa ,∀a ,b ∈ A
Equivalence relationships:
Binary relation defined on a set to any subset of the Cartesian product AxA and
R⊂ AxA
Properties
The binary relations can have the following propertiesif
•Reflexive:: a Ra , ∀a ∈ A
•Symmetric: if a Rb ⇔ bRa
•Antisymmetric: if a Rb and bRa ⇒ a = b
•Transitive :if a Rb and bRc ⇒ aR
c•Associated : if a Rb ó bRa ,∀a ,b ∈ A
Equivalence relationships:
A binary relation is said equivalence, if it satisfies the properties reflexive, symmetric and transitive
Equivalence classes: Equivalence class is called an element If a ∈ A and is denoted by cl(a) the subset consisting of all elements of the set the subset consisting of all elements of the set associated with it.
cl(a) = { x ∈ A / xRa}
Equivalence classes: Equivalence class is called an element If a ∈ A and is denoted by cl(a) the subset consisting of all elements of the set the subset consisting of all elements of the set associated with it.
cl(a) = { x ∈ A / xRa}
Properties
• No type is empty, with a ∈ cl ()
• Items belonging to the same class are interrelated.
• Classes are disjoint, since if two classes have a common element is that they are the same class. Therefore, an equivalence class is defined by "any" of its elements.
Conclusion: When defining an equivalence relation on a set, every element of the set is in a class and only one.
Quotient set: Any equivalence relation defined on a set, it creates a partition into equivalence classes. The set consists of all equivalence classes is called the quotient set. Designating porA / R.
Order relationships
They can be of two types
BROAD: If you meet the properties reflexive, antisymmetric and transitive.
STRICT: If you meet antisymmetric and transitive properties.
Also, if the property meets related is said to be a total order, otherwise it is a partial order.
Bounded Sets
Given a set ordered by the relation ≡ ≤ RA and SA ⊂ is then:
The subset S is said to be upper bounded and / or lower bounded if they have any upper limit and / or below respectively
EXTREMES:Let A be an ordered set and let S ⊂ A a bounded set, then it is called:
• Higher end : The lower of all upper bounds.
• Bottom end :The majority of all lower bounds.
MAXIMUM AND MINIMUM:
If
 ∃k higher end /k ∈ S ⇒k is a maximum
∃k higher end /k ∈ S ⇒k is a maximum
0.5. - ALGEBRAIC STRUCTURES
Internal composition law:
Given a nonempty set A, is called internal composition law or "internal operation" to the application:
f : A × A → A/c = f (a ,b ) , a ,b, c ∈ A
Generally, these laws of composition or operations are denoted with symbols ∗, ⊥, ∆,+,⋅,… and is written for example c = f(a,b) = a∗b .
Any law of internal composition, for example *, can have the following properties:
• Associative: a∗(b∗c) = (a∗b)∗c ∀a, b,c ∈ A
•Commutative: a∗b = b∗a ,∀a ,b ∈ A
•Neutral element: ∃e ∈ A/ e∗a = a∗e = a , ∀a ∈ A
•Symmetric element : ∀a ∈A ,∃a′ ∈ A/ a∗a′ = a′∗a = e
•Idempotent elements: Those elements of the set that verify x∗ x = x
•Regular elements:

Left if x∗a= x∗b ⇒a=b
Right if a∗y =b∗y ⇒ a=b
•Distributive:Given two laws of composition,for example ∗ y ∆:

a∗(b∆c) = (a∗b) ∆ (a∗c), ∀a, b,c ∈ A ⇒∗ distributive over ∆
EXTERNAL COMPOSITION LAW :
A set equipped one or more internal composition law and / or external.
MORFISMOS among structures:
homomorphisms:
Given two structures (E,∗) and (F,∆) ,the application is called a homomorphism
f :(E,∗)→ (F,∆) /f (x∗ y) =f ( x) ∆ f ( y), ∀x, y ∈ E
properties:
•The image of the neutral element of (E,∗) ,exists is the image of the neutral element (Imf ,∆) : ∀ x∈ E, f (x) =f (x∗e) =f ( x)∆f(e)
•The image of the symmetrical element of any element (E,∗),if there is the element of the image symmetric element
(Imf ,∆) : ∀ x∈ E/ ∃x′,f (e) = f ( x∗ x′)= f ( x)∆f ( x′).
Depending on the type of application and the structures, the homomorphisms can be classified into:
∎ MONOMORPHISM: If f is injective.
∎ EPIMORPHISM: If f is surjective
∎ ISOMORPHISM: If f is bijective.
GROUPS:
Given a set G equipped with an internal operation ∗.It is said that the structure (G,∗) ,the group is if it satisfies the associative neutral element existence occurrence of symmetric element .If you also check the commutative property states that (G, *) is an abelian group or commutative.
Properties :
• The neutral element is unique.
• ∀a ∈G,∃| a′ ∈G /a∗a′ = a′∗a = e
• (a ∗b)′ =b′∗a′, ∀a,b ∈G
SUBGROUPS:
A non-empty subset S of a group (G,∗) ,it is a subgroup if have group structure. That is:
1 ∀a,b ∈ S,a∗b ∈S
2 The element e of (G,∗) belongs to S
3 ∀a ∈S, , a′ ∈S
CHARACTERISTICS OF SUBGROUPS :A nonempty subset S of a group is a subgroup (G,∗) ,if and only if:
1 ∀a,b ∈ S,a∗b ∈ S } ⇔ ∀a,b ∈ S , a ∗b′ ∈S
RINGS:
Given a set A equipped with two internal operations,+ And ×.It is said that the structure ( A,+, ×) ring is a commutative group if in order to the law +and the law ×
satisfies the associative and distributive over +.If you also check the commutative property to the latter,If further verifies the commutative property to the latter, says (A,+, ×) it is abelian or commutative ring.Whether the law in order to ×, there is a neutral element, then it is a unitary ring.
Properties:
• ∀a ∈A,a ×0 ,0 × a = 0, (0 is the neutral element of +)
• ∀a,b ∈A
a ×(-b)= (-a) × b = −(a× b)
(-a)×(-b)= a×b
NOTABLE FEATURES:
•Invertible elements : In a unitary ring ( A,+, ×) elements that symmetrical in order the law x .namely ∃a 777777 1 being the unitary element of the ring.
•Idempotent elements: These are the elements that verify ring,a× a = a .
• Nilpotent elements:These are the elements that verify Ring
an = a ×a× .......× a =0,n∈N
A non-empty subset S of a ring ( A,+, ×) is a subring if ( s,+, ×) has ring structure. That is:
1 (S,+) is a commutative subgroup
2 The law × is closed on S. Namely ,∀a ,b ∈ S, a × b ∈ S
∀a,b ∈ S
BODIES:
a-b ∈ S
a × b ∈ S
A body (K,+, ×) is a unitary commutative ring in which all elements are reversed, except 0 (neutral element of +).That is:
(K,+, ×)is⇔ (K,+) is commutative
(K,+) is commutative
(K,-{0},x) is group commutative
Properties :
•In a body there are divisors of zero because all elements other than 0 are inverse,therefore, it can be stated that (K,+, ×) body ⇒ (K,+, ×) is integral domain.
•In an equation body a x × = b/a, b ∈K ; a ≠ 0 and always have this solution is unique.
subfields
A non-empty subset S of a body (K,+, ×) is a subfield if it has body structure (S,+, ×) . That is:
1.(S,+, ×) is a subring of (K,+, ×)
2. ∀a∈S / a≠ 0 ⇒ ∃a−1∈S
∀a,b ∈S
 a -b∈S
a -b∈S
a× b−1 ∈S/b ≠ 0
a−1
The subset S is said to be upper bounded and / or lower bounded if they have any upper limit and / or below respectively
EXTREMES:Let A be an ordered set and let S ⊂ A a bounded set, then it is called:
• Higher end : The lower of all upper bounds.
• Bottom end :The majority of all lower bounds.
If
∃k bottom end /k ∈ S ⇒k is a minimum
MONOTONOUS APPLICATION
Let A and B be two ordered sets ( A,≤) And (B,≤) and the application is f: A → B, then we say that
INCREASING :x, y ∈ A /x<y ⇒f(x) ≤ f(y)
DECREASING:x, y ∈ A /x<y ⇒f(x) ≥ f(y)
By substituting the signs ≤ y ≥ by < y > respectively, f is said to be strictly monotonous
Bounded function:.
Let f: A → B/ (B,≤) is ordained, it says that the application is bounded upwards or downwards if the image set f (A) is bounded upwards or downwards respectively in B
0.5. - ALGEBRAIC STRUCTURES
Internal composition law:
Given a nonempty set A, is called internal composition law or "internal operation" to the application:
f : A × A → A/c = f (a ,b ) , a ,b, c ∈ A
Generally, these laws of composition or operations are denoted with symbols ∗, ⊥, ∆,+,⋅,… and is written for example c = f(a,b) = a∗b .
Any law of internal composition, for example *, can have the following properties:
• Associative: a∗(b∗c) = (a∗b)∗c ∀a, b,c ∈ A
•Commutative: a∗b = b∗a ,∀a ,b ∈ A
•Neutral element: ∃e ∈ A/ e∗a = a∗e = a , ∀a ∈ A
•Symmetric element : ∀a ∈A ,∃a′ ∈ A/ a∗a′ = a′∗a = e
•Idempotent elements: Those elements of the set that verify x∗ x = x
•Regular elements:
Left if x∗a= x∗b ⇒a=b
Right if a∗y =b∗y ⇒ a=b
•Distributive:Given two laws of composition,for example ∗ y ∆:
a∗(b∆c) = (a∗b) ∆ (a∗c), ∀a, b,c ∈ A ⇒∗ distributive over ∆
a∆(b∗c) = (a∆b)∗(a∆c), ∀a, b,c ∈ A ⇒∗ distributive over ∗
EXTERNAL COMPOSITION LAW :
A set equipped one or more internal composition law and / or external.
MORFISMOS among structures:
homomorphisms:
Given two structures (E,∗) and (F,∆) ,the application is called a homomorphism
f :(E,∗)→ (F,∆) /f (x∗ y) =f ( x) ∆ f ( y), ∀x, y ∈ E
properties:
•The image of the neutral element of (E,∗) ,exists is the image of the neutral element (Imf ,∆) : ∀ x∈ E, f (x) =f (x∗e) =f ( x)∆f(e)
•The image of the symmetrical element of any element (E,∗),if there is the element of the image symmetric element
(Imf ,∆) : ∀ x∈ E/ ∃x′,f (e) = f ( x∗ x′)= f ( x)∆f ( x′).
Depending on the type of application and the structures, the homomorphisms can be classified into:
∎ MONOMORPHISM: If f is injective.
∎ EPIMORPHISM: If f is surjective
∎ ISOMORPHISM: If f is bijective.
∎ ENDOMORPHISM: If (E,∗) ≡ (F,∆) .
∎ AUTOMORPHISM: If (E,∗) ≡ (F,∆) and f is bijective
GROUPS:
Given a set G equipped with an internal operation ∗.It is said that the structure (G,∗) ,the group is if it satisfies the associative neutral element existence occurrence of symmetric element .If you also check the commutative property states that (G, *) is an abelian group or commutative.
Properties :
• The neutral element is unique.
• ∀a ∈G,∃| a′ ∈G /a∗a′ = a′∗a = e
• (a ∗b)′ =b′∗a′, ∀a,b ∈G
•(a′)′ =a
•All the elements of G are regular.
SUBGROUPS:
A non-empty subset S of a group (G,∗) ,it is a subgroup if have group structure. That is:
1 ∀a,b ∈ S,a∗b ∈S
2 The element e of (G,∗) belongs to S
3 ∀a ∈S, , a′ ∈S
CHARACTERISTICS OF SUBGROUPS :A nonempty subset S of a group is a subgroup (G,∗) ,if and only if:
1 ∀a,b ∈ S,a∗b ∈ S } ⇔ ∀a,b ∈ S , a ∗b′ ∈S
2 ∀a ∈ S ,a′ ∈ S
„RINGS:
Given a set A equipped with two internal operations,+ And ×.It is said that the structure ( A,+, ×) ring is a commutative group if in order to the law +and the law ×
satisfies the associative and distributive over +.If you also check the commutative property to the latter,If further verifies the commutative property to the latter, says (A,+, ×) it is abelian or commutative ring.Whether the law in order to ×, there is a neutral element, then it is a unitary ring.
Properties:
• ∀a ∈A,a ×0 ,0 × a = 0, (0 is the neutral element of +)
• ∀a,b ∈A
a ×(-b)= (-a) × b = −(a× b)
(-a)×(-b)= a×b
NOTABLE FEATURES:
•Invertible elements : In a unitary ring ( A,+, ×) elements that symmetrical in order the law x .namely ∃a 777777 1 being the unitary element of the ring.
•Idempotent elements: These are the elements that verify ring,a× a = a .
• Nilpotent elements:These are the elements that verify Ring
an = a ×a× .......× a =0,n∈N
•Zero divisors: Are nonzero elements that verify ring, a×b= b× a =0.
RINGS OF INTEGRITY:
Is a ring without zero divisors. If a ring is unitary and integrity is called commutative integral domain.
SUBRINGS:
A non-empty subset S of a ring ( A,+, ×) is a subring if ( s,+, ×) has ring structure. That is:
1 (S,+) is a commutative subgroup
2 The law × is closed on S. Namely ,∀a ,b ∈ S, a × b ∈ S
∎ SUBRING CHARACTERIZATION : A subset S is nonempty subring (A,+, ×) is a subring if only if:
BODIES:
a-b ∈ S
a × b ∈ S
A body (K,+, ×) is a unitary commutative ring in which all elements are reversed, except 0 (neutral element of +).That is:
(K,+, ×)is⇔
(K,-{0},x) is group commutative
The law ×is distributive over the law +
Properties :
•In a body there are divisors of zero because all elements other than 0 are inverse,therefore, it can be stated that (K,+, ×) body ⇒ (K,+, ×) is integral domain.
•In an equation body a x × = b/a, b ∈K ; a ≠ 0 and always have this solution is unique.
subfields
A non-empty subset S of a body (K,+, ×) is a subfield if it has body structure (S,+, ×) . That is:
1.(S,+, ×) is a subring of (K,+, ×)
2. ∀a∈S / a≠ 0 ⇒ ∃a−1∈S
∎CHARACTERIZATION subfields: A non-empty subset S of a body (K,+, ×) is a subfield if only if:
∀a,b ∈S
a× b−1 ∈S/b ≠ 0
a−1