NUMBER PATTERNS AND SEQUENCES TUTORIAL

NUMBER PATTERNS AND SEQUENCES TUTORIAL

Subject : Mathematics Form 1

and To get the document in MS word file


=
View


To Get more DOWNLOAD 






IN WORD DOCS

 or see it on gooogle doc

Learning Objective : Number Patterns and Number Sequences Learning Outcomes : 1. Identify patterns of number sequences. 2. Extend, complete and construct number sequences. 3. Recognize odd and even numbers and explore their general properties. 4. Identify prime numbers. 5. Understand factors and prime factors. 6. Find the common factors and highest common factors (HCF). 7. Understand multiples. 8. Find the common multiples and lowest common multiples (LCM

2.1 Number Patterns & Number Sequences - A list of numbers that follow a certain pattern is called number sequence. - In a number sequence, we can see how the number pattern is form.


To see the lesson in MS word form
DOWNLOAD hERE

1. 3, 7, 11, 15, 19 Pattern : begin with 3 and add 4 to the number before it (+4) 2. 305, 300, 295, 290, 285 Pattern : begin with 305 then minus / subtract 5 from the number before it (- 5) 3. 2, 6, 18, 54, 162 Pattern : begin with 2, then multiply each number by 3 (x3) 4. 64, 32, 16, 8, 4 Pattern : begin with 64 then divide each number by 2 (÷ 2)

Complete the missing number in the n

List the number sequences for these number sequences 1. 3, 6, 9 , 12, 15 , 18 Pattern : + 3 2. 64, 56, 48, 40, 32, 29 Pattern : - 8 3. 7, 21, 63, 189, 567, 1761 Pattern : x 3 4. 800, 400, 200, 100, 50, 25 Pattern : ÷ 2

umber patterns

1. List down the whole numbers between 30 to 37 31, 32, 33, 34, 35, 36 2. Add 5 to whole numbers from 3 to 28 3, 8, 13, 18, 23, 28 3. Subtract 3 from whole number from 13 to 1 13, 10, 7, 4, 1 4. Multiply 4 to whole numbers from 2 to 128 2, 8, 32, 128

2.2 Even Numbers & Odd Numbers

- Even numbers are whole numbers that can be divided by 2 exactly (no remainder). Example: 2, 4, 6, 8, 10, … - Odd numbers are whole numbers that cannot be divided by 2 exactly (has remainder). Example: 1, 3, 5, 7, 9, 11, … - ‘0’ is neither an add number nor an even number Determine whether these numbers are even numbers or odd numbers 1. 214 214 ÷ 2 = 107 therefore 214 is an even number 2. 735 735 ÷ 2 = 367 remainder 1 therefore 735 is an odd number 3. 2 579 2 579 ÷ 2 = 1 289 remainder 1 therefore 2 579 is an odd number 4. 5 550 5 550 ÷ 2 = 2 775

2.3 Prime Numbers

- Prime number is a whole number that can only be divided by itself and number 1 - The number 1 is not a prime number because it can only be divided by itself - All the prime numbers are odd numbers except for 2 - Example : 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, … Determine whether this number is a prime number or not 1. 31 31 ÷ 1 = 31 31÷ 31 = 1 31 can only be divided by 1 and itself. 31 is a prime number 2. 65 65 ÷ 1 = 65 65 ÷ 65 = 1 65 ÷ 5 = 13 65 can be divided by 1, itself and also 5. 65 is not a prime number 3. 71 71 ÷ 1 = 71 71÷ 71 = 1 71 can only be divided by 1 and itself. 71 is a prime number 4. 93 93 ÷ 1 = 93 93 ÷ 93 = 1 93 ÷ 3 = 31 93 can be divided by 1, itself and 3. 93 is not a prime number

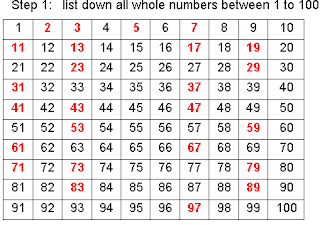
Sieve Of Erastosthenes - A method of finding prime numbers between 1 to 100 (25 numbers) Step 1: list down all whole numbers between 1 to 100

  Whole numbers photo

Step 2: Cross out 1, because 1 is not a prime number. Step 3: Circle 2 and cross out all numbers that can divided by 2. Step 4: Circle 3 and cross out all numbers that can divided by 3. Step 5: Circle 5 and cross out all numbers that can divided by 5. Step 6: Circle 7 and cross out all numbers that can divided by 7. Step 7: Circle all remaining numbers and list down. The remaining numbers are the prime numbers between 1 to 100. Answer: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.

http://www.4shared.com/file/125589473/1f7766d0/math_tests__School_exams_e.html

2.4 Factors

- A factor of a given number is the number that can divide the given number exactly without any remainder. - The number 1 is a factor of all numbers. - Every number is a factor of itself - A whole number may have more than 2 factors. List all the factors of these numbers 1. 6 1 x 6 factors of 6 = 1, 2, 3, 6 2 x 3 2. 18 1 x 18 factors of 6 = 1, 2, 3, 6, 9, 18 2 x 9 3 x 6 3. 45 1 x 45 factors of 6 = 1, 3, 5, 9, 15, 45 3 x 15 5 x 9 4. 88 1 x 88 factors of 6 = 1, 2, 4, 8, 11, 22, 44, 88 2 x 44 4 x 22 8 x 11 Determine whether 1. 9 is a factor of 54 54 ÷ 9 = 6 (exact division, no remainder) Therefore 9 is a factor of 54 2. 7 is a factor of 48 48 ÷ 7 = 6 remainder 6 (not exact division) Therefore 7 is not a factor of 48

2.5 Prime Factors

- Prime factors of a given number are factors which are also prime numbers. - Example: Factors of 6: 1, 2, 3, 6 Prime numbers: 2 and 3 Prime factors of 6: 2 and 3 List all the prime factors of these numbers. 1. 24 Method 1 : List the factors Factors of 24 : 1, 2, 3, 4, 6, 8, 12, 24 Prime Factors : 2 and 3

Method 2 : Continuous Division

https://docs.google.com/exercises

Determine whether

1. 2 is a prime factor of 18 18 ÷ 2 = 9 (exact division, no remainder) Therefore 2 is a prime factor of 18 2. 7 is a factor of 46 46 ÷ 7 = 6 remainder 4 (not exact division) Therefore 7 is not a prime factor of 46 3. 4 is a factor of 200 200 ÷ 4 = 50 (exact division, no remainder) 4 is a factor of 200 but 4 is not a prime number Therefore 4 is not a prime factor of 200

.6 Common Factors & Highest Common Factors (HCF)

Common Factors - Common factor is a number that is a factor of two or more numbers. - 1 is a common factor of all numbers. Find all the common factors of these numbers. 1. 8 and 12 Factors of 8 : 1, 2, 4, 8 Factors of 12 : 1, 2, 3, 4, 6, 12 Common factors of 8 and 12 : 1, 2, 4 2. 6, 12 and 18 Factors of 6 : 1, 2, 3, 6 Factors of 12 : 1, 2, 3, 4, 6, 12 Factors of 18 : 1, 2, 3, 6, 9, 18 Common factors of 6, 12 and 18: 1, 2, 3, 6 3. 27, 36 and 81 Factors of 27 : 1, 3, 9, 27 Factors of 36 : 1, 2, 3, 4, 6, 9, 12, 18, 36 Factors of 81 : 1, 3, 9, 27, 81 4. Common factors of 27, 36 and 81: 1, 3, 9 Determine whether 1. 6 is a common factor of 12, 18 and 24 12 ÷ 6 = 2 (exact division, no remainder) 18 ÷ 6 = 3 (exact division, no remainder) 24 ÷ 6 = 4 (exact division, no remainder) Therefore 6 is a common factor of 12, 18 and 24 2. 9 is a common factor of 63 and 120 63 ÷ 9 = 7 (exact division, no remainder) 120 ÷ 9 = 13 remainder 3 (not exact division) Therefore 9 is a not common factor of 63 and 120
Highest Common Factors ( HCF )
- HCF of two or more numbers is the largest common factor of these numbers.

2.7 Multiples

- The multiples of a number is the product of that number with any whole number except

zero.

- Multiples are also a sequence.

List the first five multiples of these numbers.

1. 3

3 x 1 = 3

3 x 2 = 6

3 x 3 = 9

3 x 4 = 12

3 x 5 = 15

The first five multiples of 3 are 3, 6, 9, 12 and 15

2. 9

9 x 1 = 9

9 x 2 = 18

9 x 3 = 27

9 x 4 = 36

9 x 5 = 45

The first five multiples of 3 are 9, 18, 27, and 45

List all the multiples of these numbers.

1. Multiples of 2 between 13 to 27

14, 16, 18, 20, 22, 24, 26

2. Multiples of 5 from 50 to 70

50, 55, 60, 65, 70

Determine whether

1. 48 is a multiple of 4

48 ÷ 4 = 12 (exact division, no remainder)

Therefore 48 is a multiple of 4

2. 26 is a multiple of 3

26 ÷ 3 = 3 remainder 2 (not an exact division, has remainder)

Therefore 26 is not a multiple of 3

2.6 Common Multiples & Lowest Common Multiples (LCM)

Common Multiples
- Common multiple is a number that is a multiple of two or more numbers.

- Example 8 is a common multiple of 2 and 4

Multiple of 2 : 2, 4, 6, 8, 10, 12 ,… ( 8 is multiple of 2 )

Multiple of 4 : 4, 8, 12, 16, 20, … ( 8 is multiple of 4 )

Therefore 8 is a common multiple of 2 and 4

Find the first three common multiples of these numbers.

1. 2 and 3

Multiple of 2 : 2, 4, 6, 8, 10, 12 , 14, 16, 18, 20, …

Multiple of 3 : 3, 6, 9, 12, 15, 18, 21, 24, …

Therefore the first three common multiples of 2 and 3 are 6, 12, and 18

2. 3, 4 and 6

Multiple of 3 : 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36,..

Multiple of 4 : 4, 8, 12, 16, 20, 24, 28, 32, 36, ..

Multiple of 6 : 6, 12, 18, 24, 30, 36, ..

Therefore the first three common multiples of 3, 4 and 6 are 12, 24 and 36

Determine whether

1. 50 is a common multiple of 2 and 5

50 ÷ 2 = 25 (exact division, no remainder)

50 ÷ 5 = 10 (exact division, no remainder)

Therefore 50 is a common multiple of 2 and 5

2. 120 is a common multiple of 3, 4 and 9

120 ÷3 = 40 (exact division, no remainder)

120 ÷4 =30 (exact division, no remainder)

120 ÷ 9 = 13 remainder 3 (not exact division)

Therefore 120 is not a common multiple of 3, 4 and 9

\

http://www.4shared.com/file/125589473/1f7766d0/math_tests__School_exams_e.html

Lowest Common Multiples ( LCM )
- LCM of two or more numbers is the smallest common multiple of these numbers.

Find the LCM of the followings.

1. 6 and 36

Method 1 : Listing the multiples

Multiple of 6 : 6, 12, 18, 24, 30, 36, .

Multiple of 9 : 9, 18, 27, 36, …

The LCM of 6 and 9 is 18

and a math test   https://docs.google.com/math exercises
whole number lesson

https://docs.google.com/leaf?id=1WxPw2LhqeyNK0wrONdEjm2bgsBcPadqKXloY6ZxdiAx2XFfAncqb7TOtrkuh&sort=name&layout=list&num=50

Please leave your comments and notices here below